- 丸みを帯びた五芒星を描くアニメーションをgnuplotで作成
- 曲線の数式から読み取れるフーリエ級数っぽさから考えた改造のアイデア
- 2組の回転円が曲線を描くアニメーションの作成とプログラムの中身を解説
どうも、Hiro (@hiroloquy) です。
先日、Twitter上で千葉大数学科18 (@chibamath18) さんのとあるツイートを見つけ、gnuplotでプログラムを作成、TwitterとGitHubで公開しました。
以前、Twitterでバズっていたリンク機構をgnuplotで再現しました。
そのとき、ある完成形を真似るために手を動かすことで、自分のgnuplotノウハウが深まり、スクリプトの表現の幅が広がるのを実感しました。
そのとき再現したリンク機構に関する投稿がこちら▼▼▼
そこで今回は、gnuplotで丸みを帯びた五芒星を描いてみようと思います。
ただ曲線のアニメーションはカンタンなのである改造してみました。
記事を読んでいただけると幸いです。
「丸みを帯びた五芒星」の数式（媒介変数表示）
今回扱う「丸みを帯びた五芒星」を表す媒介変数表示は元ツイートにあったのでそれを参考にしました（$t$ はパラメータ）。
$$
\begin{cases}
x(t)=2\sin 2t – \cos 3t\\
y(t)=\sin 3t – 2 \cos 2t
\end{cases}\label{eq:parametric}
$$
三角関数$\sin$、$\cos$のみで構成されたシンプルな式で五芒星が描けるのはすごいですね。
gnuplotでプログラムを作成
丸みを帯びた五芒星を描くプログラムがこちらです（GitHubで公開しています）。
▼▼▼
このプログラムは水滴リンク機構で作ったプログラムを流用していて、90%ぐらい同じです。
水滴リンク機構のプログラムの下記3点を修正すると、今回のプログラムが完成します。
- 変数名を一部変更
- リンク描画用のテキストデータの出力部分を削除
- リンク機構の点$\mathrm{P}$の座標を式 ($\ref{eq:parametric}$) に変更
gnuplotのライブラリ的なものが自分の中で出来てきた感じがして少し感動しました。「塵も積もれば山となる」ですね。
出力画像からGIFデモを作成
pltファイル中のPrameterにあるqtModeをqtMode==0にすると、ターミナルはpngcairoに切り替わってフォルダpngを生成し、その中にPNG画像 img_xxxx.png を出力します。
PNG画像をGIF動画に変換するために、私はFFmpegを使用しました。コマンドはQiitaのこちらの記事を参考にしました。
1行目でcdコマンドでディレクトリをpngフォルダに移動し、2行目でFFmpegを実行するとまずdemo.mp4が生成され、さらに3行目を実行するとその動画を使ってdemo.gifを生成します。
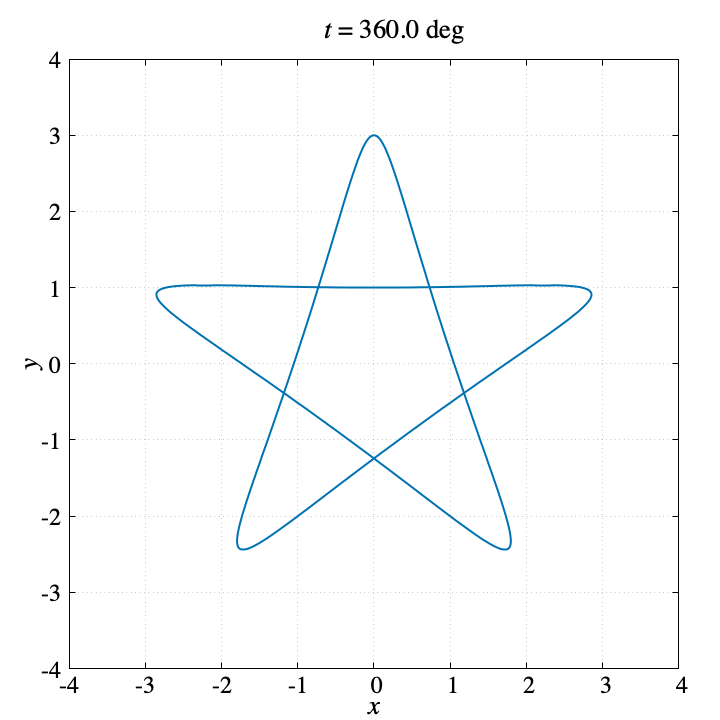
上記コマンドを使って生成したGIF動画が左側です。また右側はプログラム終了時に生成する軌跡のPNG画像です。
img_xxx.png → demo.gif 
trajectory_plot.png
gnuplotではターミナルでgifを選べばGIFアニメを生成できますが、pngcairoでPNG画像を生成するといろんな使い方ができるのでgnuplotでアニメーションを作るならpngcairoにして、FFmpegを使うのがオススメです。
- スナップショットとして画像を使用
- FFmpegを使えばGIF、MP4形式の動画を生成
今回作ったプログラムの開発環境はこちらです。
- macOS Big Sur 11.3.1 / Macbook Air (M1, 2020) 16GB
- gnuplot version 5.4 patchlevel 1
- VScode 1.56.2
- ffmpeg 4.4
フーリエ級数風の描画アニメーションに改造！
これでgnuplotで丸みを帯びた五芒星を再現できました。以前の記事では再現することで満足していましたが、今回は元ネタを少し改造します。
数式の特徴から生まれた改造のアイデア
五芒星の式 ($\ref{eq:parametric}$) の特徴は前述のとおり、$x(t)$、$y(t)$ともに$\sin t$、$\cos t$で構成されています。そしてそれらを定数倍し、和をとることで式が作られています。
そこで、$x(t)$、$y(t)$を項数が2個のフーリエ級数と見立てると、回転する２つの円によって曲線を描くアニメーションを作ることができます。
1次元 ($y=f(x)$) の場合は自身のYouTubeチャンネルでプログラムを紹介していますが、今回は2次元 ($x(t)$、$y(t)$) なので回転する円の組を各座標で準備する必要があります。（必要な円の個数は 2項×2軸=4個）
ポチップ
プログラムを改変
前述のプログラムを改変したものがこちらです。
大きく追加修正を施した箇所は96 – 124行目です。$x(t)$、$y(t)$それぞれ２つの三角関数の和で表されるので合計４個の円が必要でした。
フーリエ級数の動画でよく見る回転円の描き方
円を描くのに必要な座標の求め方について $x(t)$ を例に簡単に説明します（96 – 109行目）。cx1_x、cx1_yは $x(t)$ を描く円の1個目（式の第1項）、cx2_x、cx2_yが2個目の中心座標です。これらを計算するときは３つのベクトルを加算することで求めます。
$$
\begin{bmatrix}0\\ \mathrm{offsetXtCircle}\end{bmatrix}\ \ ,\ \ \begin{bmatrix}2\sin 2t\\ 2\cos 2t\end{bmatrix}\ \ ,\ \ \begin{bmatrix}-\cos 3t\\ -\sin 3t\end{bmatrix}
$$
1つ目のベクトルの offsetXtCircle はどれだけ原点から遠ざけて円を描くかを決めるパラメータです。2つ目と3つ目のベクトルの $x$ 成分は $x(t)$ の項です。一方 $y$ 成分は $\sin$ と $\cos$ を反転させたものを書いています。このように書くことで回転する点や円を描くことができます。
あとは set object circle で円を描き、set arrow nohead で半径を描けば十分です。縁の半径は各項の係数です。半径を描くのは回転の様子がわかるためです。
GIF画像にして動作を確認
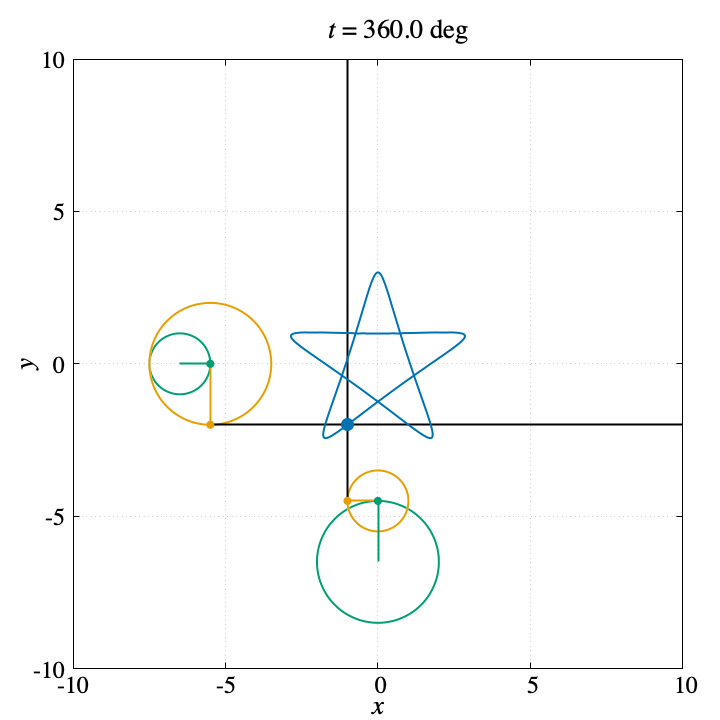
前述と同様の方法でGIF画像を作ると、良いアレンジが加わった動画を作ることができます。
img_xxx.png → demo_with_circles.gif 
trajectory_plot_with_circles.png
$x(t)$ を描くために回る円の周上の点と、$y(t)$ を描くために回る円の周上の点それぞれから各軸と平行な直線を引くことで、2直線の交点が曲線を描くアニメーションを作ることができました。
今回は項数が2個と少なかったので、プログラムでは円の座標や半径を表す線をすべて書き出していますが、2項間の係数（または位相）にあえて規則性を与えて一般項を作れば、配列と for 文で処理することも可能です。
今回作った２つのスクリプトを動画にまとめてYouTubeにアップしているので、よければ高評価とチャンネル登録をよろしくお願いします。
まとめ
今回は @chibamath18 さんがツイートした曲線のアニメーションをgnuplotで作りました。
そして数式の特徴を利用して、回転する円で曲線を描くアニメーションを作ってみました。
今回作成したスクリプトとデモGIFは私のGitHubでも公開しています。英語で書いたREADMEもあるので、そちらも参考にしてみてください。
ポチップ
コメント