【gnuplot】水滴の軌跡を描くリンク機構のプログラムを解説

どうも、Hiro (@hiroloquy) です。

先日、Twitter上で上木 敬士郎 Keishiro Ueki (@ChocoLinkage) さんのとあるツイートを見つけ、gnuplotでプログラムを作成、TwitterとGitHubで公開しました。

このツイートの左側にある、水滴を描くリンク機構をgnuplotで再現しました。スクリプトはGitHubで公開中。https://t.co/mmewa3Hto6

よければ実行してみてください。
READMEには導出した各点の座標も書いてます。#gnuplot #github https://t.co/4ZM7UY9BZA pic.twitter.com/2IICVWyouc

— Hiro (@hiroloquy) June 4, 2021

元ツイートでは、水滴のような軌跡を描くリンク機構を2パターン紹介していました。左側の機構は右側のものよりもリンク数が少なく、「モデリングして再現しやすそう！」と考えました。

そこで本記事では左側のリンク機構を取り上げ、プログラムを作るまでの過程について解説します。よければ記事を読んでいただけると幸いです。

元ツイートからリンク機構の情報を読み取りモデリング

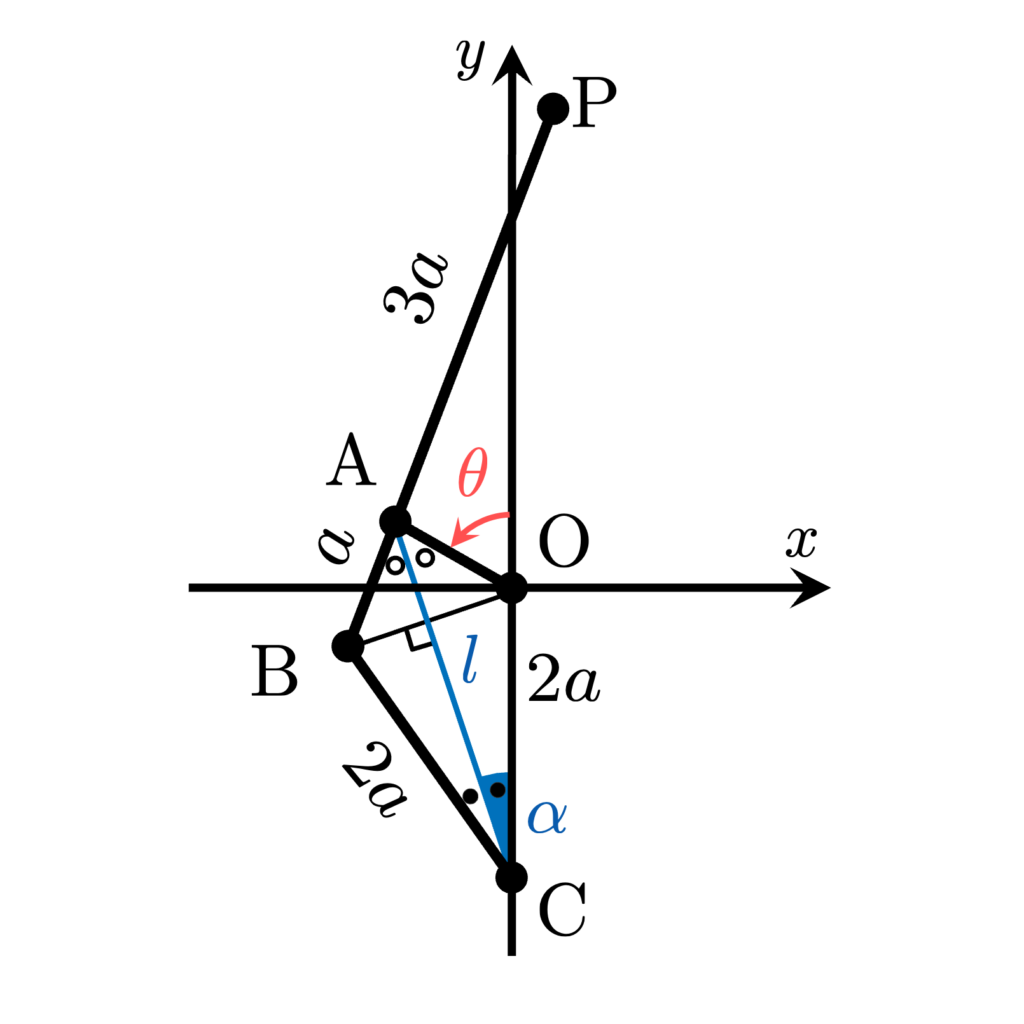
元のツイートのアニメーションから、下図のようなモデルを考えました。

このリンク機構の特徴的な点は合計5個。$\mathrm{O}$と$\mathrm{C}$は固定、$\mathrm{A}$と$\mathrm{B}$はフリージョイント、$\mathrm{P}$が軌跡を描く点となります。また、リンク$\mathrm{OA}$が$\mathrm{O}$を中心に回転するから、$\mathrm{O}$を原点とする$xy$平面を考えます。

リンクの長さについては各リンクの長さの比の関係がわかれば十分です。元ツイートから、リンクの長さの比はおそらくこちら。

$$
\mathrm{OA}:\mathrm{AB}:\mathrm{OB}:\mathrm{OC}:\mathrm{AP}=1:1:2:2:3\label{eq:ratio}
$$

この関係が正しいとすると、$\triangle{\mathrm{OAB}}$と$\triangle{\mathrm{OBC}}$は二等辺三角形になるため、線分$\mathrm{AC}$は２つの二等辺三角形の垂直二等分線となります。そこで、線分$\mathrm{AC}$の長さを$l$、$\angle\mathrm{OCA}$の値を$\alpha$とします（文字でおいたのは後の計算で多用するため）。

そして最後に、点$\mathrm{P}$が軌跡を描くために常に回り続ける線分$\mathrm{OA}$の回転角を$\theta$とします。一般的に$\theta$の基準は$x$軸を取りますが、今回扱うリンク機構の軌跡は$y$軸対称なので、$y$軸を基準にしました。

ジョイントやリンクの長さ、パラメータなどに文字を定義するのはこの辺でいいでしょう。
次は4つの点$\mathrm{A}$、$\mathrm{B}$、$\mathrm{C}$、$\mathrm{P}$の座標の導出過程を説明します。

三角関数とベクトルを駆使してジョイントの座標を導出

では4つの点の座標を求めていきましょう

点$\mathrm{C}$を計算

一番簡単なのが点$\mathrm{C}$です。固定点なので $x$ 座標、$y$ 座標はともに定数で $\theta$ を含まないことがわかります。図を見れば以下の座標になるのは一目瞭然です。

$$\overrightarrow{\mathrm{OC}}=\begin{bmatrix}0 \\ -2a\end{bmatrix}\label{eq:c}$$

点$\mathrm{A}$を計算

回転するリンク$\mathrm{OA}$の長さと角度を使えば、座標は次のように求められます。$\theta$ の基準が $y$ 軸であることを忘れずに。

$$
\overrightarrow{\mathrm{OA}} = \begin{bmatrix}-a\sin\theta \\ a\cos\theta\end{bmatrix}
$$

点$\mathrm{B}$を計算

点$\mathrm{B}$は少し厄介ですが、モデルの図をみて幾何関係に着目すれば大丈夫です。原点 $\mathrm{O}$から点$\mathrm{B}$までの道のりは次の2通り。

$$\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CB}}\label{eq:vec_b}$$

どちらかの式を使うかについてですが、点 $\mathrm{C}$ が $\theta$ に依らないことを利用するために、今回は後者の式から点$\mathrm{B}$の座標を求めます。長さ $2a$ のリンク $\mathrm{BC}$ は $y$ 軸の正の方向と角度 $2\alpha$ をなすので

$$\overrightarrow{\mathrm{CB}}=\begin{bmatrix}-2a\sin 2\alpha\\ -2a\cos 2\alpha\end{bmatrix}\label{eq:cb}$$

式($\ref{eq:c}$)を利用すると、点$\mathrm{B}$の座標は次のように書き表されます。

$$\overrightarrow{\mathrm{OB}}=\begin{bmatrix}0\\-2a\end{bmatrix}+\begin{bmatrix}-2a\sin 2\alpha\\ -2a\cos 2\alpha\end{bmatrix}=\begin{bmatrix}-4a\cos\alpha\sin\alpha\\-4a\cos^2\alpha\end{bmatrix}\label{eq:ob}$$

この式の中の $\alpha$ が $\theta$ を使ってどう表されるか考える必要があります。$\cos\alpha$ と $\sin\alpha$ にはピタゴラスの基本三角関数公式の関係があるので、どちらか一方を求めます。

$$\cos^2\alpha+\sin^2\alpha=1\label{eq:kihon}$$

【注意】逆三角関数 $\arccos$、$\arcsin$をあえて使わないのは定義域、値域の関係でプログラムがエラーを出るのを避けるためです。

$\triangle{\mathrm{OAC}}$に着目して余弦定理を用いると、$\cos\alpha$ に関する式が次のように成立します。

$$\cos\alpha = \frac{l^2+(2a)^2-a^2}{2\cdot l\cdot 2a} = \frac{l^2+3a^2}{4al}\label{eq:cosa}$$

次に式($\ref{eq:kihon}$) から $\sin\alpha$ を求めますが、$\cos\alpha$ の2乗を外すので $\sin\alpha$ の符号を考えなければいけません。

$\alpha$ とリンク$\mathrm{OA}$ の位置関係から、$\theta$ と $\alpha$ には次のような符号の関係があることがわかります。

$$\begin{cases}
0^\circ\leq\theta\leq180^\circ:&\alpha\geq 0\\
180^\circ<\theta<360^\circ:&\alpha<0
\end{cases}$$

これより、$\sin\alpha$ の符号に関する場合わけは次式のようになります。

$$\sin\alpha = \begin{cases}\ \ \ \sqrt{1-\cos^2\alpha}\ \ \left(\ \ \ \ 0^\circ\leq\theta\leq 180^\circ\right)\\-\sqrt{1-\cos^2\alpha}\ \ \left(180^\circ<\theta<360^\circ\right)\end{cases}\label{eq:sina}$$

まずは $\alpha$ と $l$ の関係がわかったので、次は $l$ と $\theta$ の関係を求めます。再び$\triangle{\mathrm{OAC}}$に着目して余弦定理を用いると

$$\begin{align}l^2 &= a^2+(2a)^2-2\cdot a\cdot 2a \cos\left(\pi-\theta\right)=5a^2+4a^2\cos\theta\\
l&=a\sqrt{5+4\cos\theta}\ \ \left(\because a\geq 0\right)\label{eq:l}\end{align}$$

式($\ref{eq:l}$)によって$l$と$\theta$の関係が分かったので、式($\ref{eq:cosa}$)、($\ref{eq:sina}$)から$\alpha$と$\theta$の関係もわかります。

つまり、式($\ref{eq:ob}$)の各成分は$\theta$を使って求められます！式を代入すると$\alpha$、$l$を消去することができますが、式が煩雑になるため今回は式($\ref{eq:ob}$)のままにします。

点$\mathrm{P}$を計算

点$\mathrm{B}$の長い導出過程を頑張ったおかげで点$\mathrm{P}$は簡単に求めることができます。式(\ref{eq:ratio})の比の関係を使えば点$\mathrm{P}$の座標は次式から求められます。ただし、点$\mathrm{B}$の式が複雑になるので、ここでも省略します。

$$\begin{align}\overrightarrow{\mathrm{OP}}&=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}}= \overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{BA}}= 4\overrightarrow{\mathrm{OA}}-3\overrightarrow{\mathrm{OB}}\\
\therefore\overrightarrow{\mathrm{OP}} &= \begin{bmatrix}-4a\sin\theta+12a\cos\alpha\sin\alpha \\ 4a\cos\theta+12a\cos^2\alpha\end{bmatrix}\end{align}$$

gnuplotでプログラムを作成

モデリングにより求めたリンク機構の各ジョイントの座標を計算し、グラフ上に描画するプログラムがこちらです。

特徴1：直線を描くのはset arrowではなくplotコマンド

gnuplotで直線を描く際、標準機能のset arrow nohead を使います。その場合、リンク$\mathrm{OA}$、$\mathrm{CB}$、$\mathrm{BP}$の3本分のarrowを用意すれば十分です。

3本のarrowを描くだけなら特に問題ありませんが、テオヤンセン機構のように10本以上のリンクで構成される場合、計算・描画の処理が重くなるためおすすめしません。

そこで今回はグラフの線を使って、つまりコマンドplotを使ってリンクを描こうと考えました。gnuplotはtxtデータを読み込んでグラフを描画するのが得意なので、set arrowよりもplotの方が処理が軽いです。そこで draw_linkage.txt にジョイントの位置座標をブロック状にまとめ、plot usingでデータを参照して描画することにしました。

ただしdraw_linkage.txt内の各ブロックにある点$\mathrm{P}$の座標を参照して点$\mathrm{P}$の軌跡を描こうと思いましたができませんでした…。ファイルが増えるのは面倒ですが、軌跡を描くためのtxtデータdraw_p_trajectory.txtを別で用意しました。

特徴2：qtModeでターミナルを簡単に切り替え

qtModeを使ってターミナルタイプをqtまたはpngcairoに切り替えることができます。

qtターミナルを選択した場合（qtMode == 1）、gnuplot は qt window を開き、このシミュレータを実行することができます。qtウィンドウの描画速度はpauseコマンドで調整できます。

pause 0.001     # Adjust the drawing speed

一方、pngcairoを選択した場合（qtMode != 1）はシミュレーションのPNG画像が出力されます。出力された画像を使えば動画やアニメーションGIFを作ることができます。

出力画像からGIFデモを作成

pltファイル中のPrameterにあるqtModeをqtMode==0にすると、ターミナルはpngcairoに切り替わってフォルダpngを生成し、その中にPNG画像を出力します。

PNG画像をGIF動画に変換するために、私はFFmpegを使用しました。コマンドはこちらの記事の2. グローバルパレットを使用して最適化を参考にしました。

ffmpegでとにかく綺麗なGIFを作りたい - Qiita

何かを説明するときにGIFってわかりやすいですよね。友達がmeeemoというサービスを作りそれのプレビュー動画を撮るお手...

qiita.com

1行目でcdコマンドでディレクトリをpngフォルダに移動し、2行目でFFmpegを実行するとまずdemo.mp4が生成され、さらに3行目を実行するとその動画を使ってdemo.gifを生成します。

上記コマンドを使って生成したGIF動画が左側です。また右側はプログラムの最後で生成する軌跡のPNG画像です。

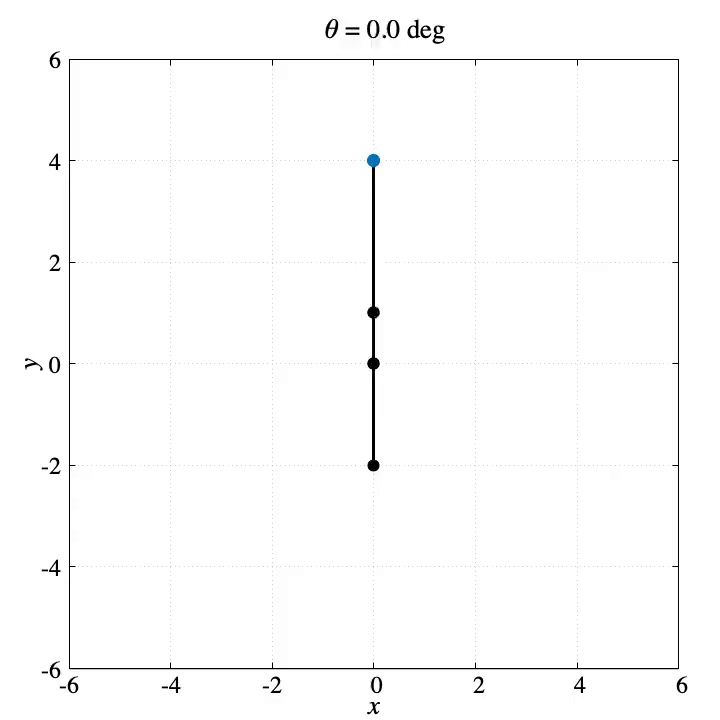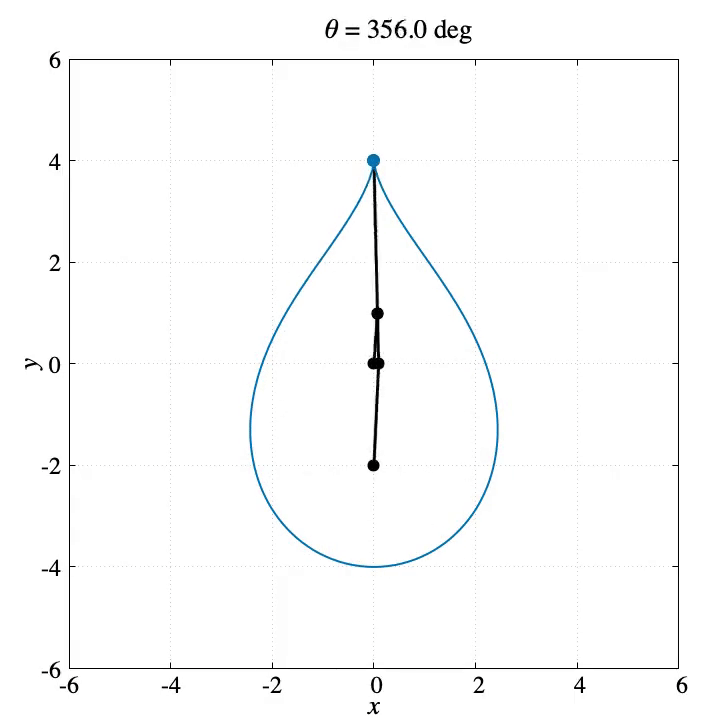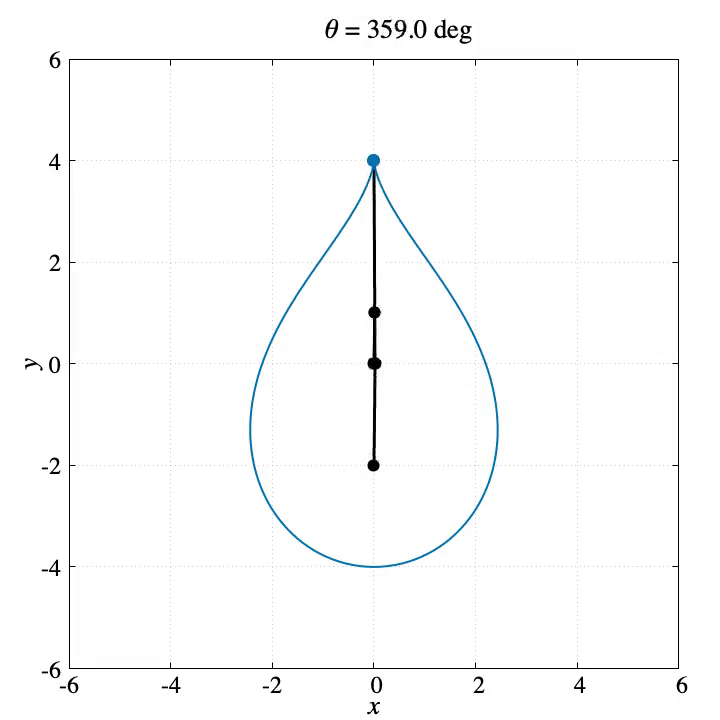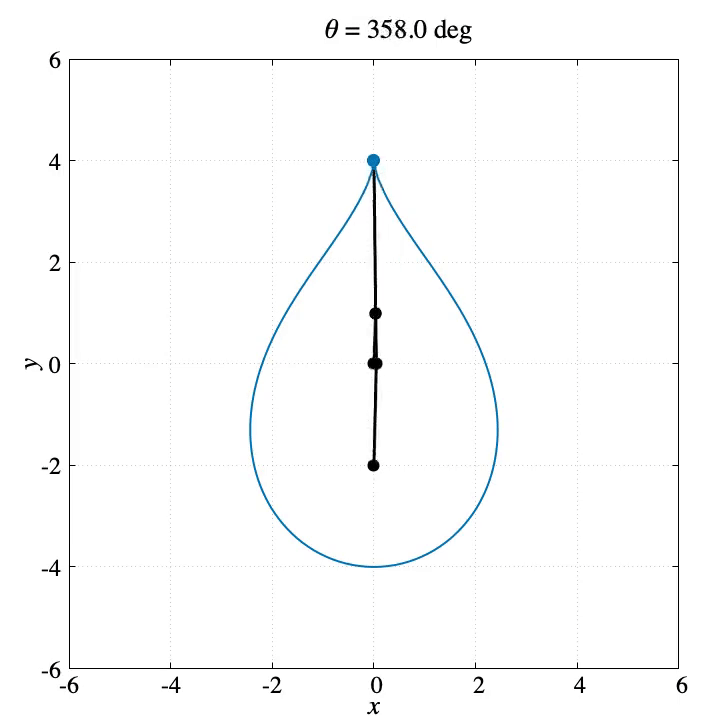
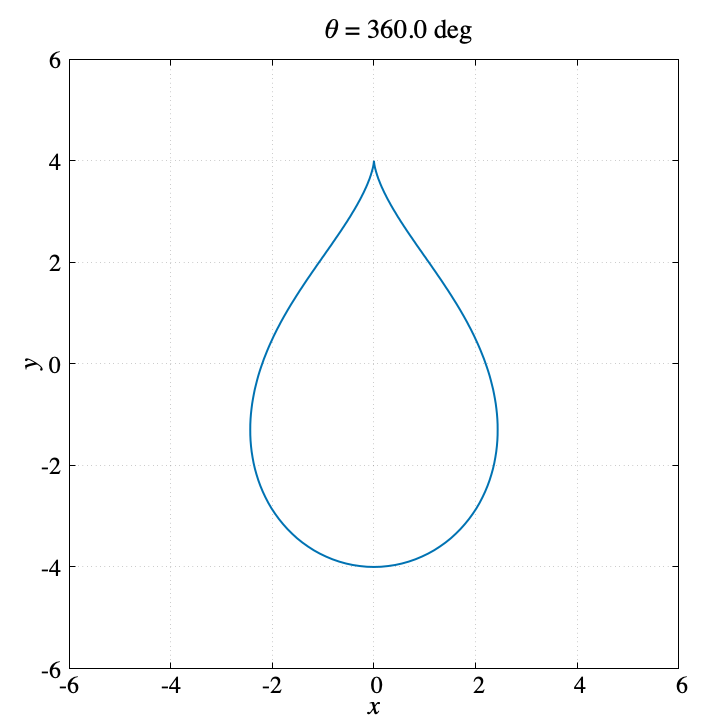
gnuplotではターミナルでgifを選べばGIFアニメを生成できますが、pngcairoでPNG画像を生成するといろんな使い方ができるのでgnuplotでアニメーションを作るならpngcairoにして、FFmpegを使うのがオススメです。

今回作ったプログラムの開発環境はこちらです。

モデリングとリンク機構の挙動をまとめた動画をYouTubeにアップロードしたので、よければ高評価とチャンネル登録をよろしくお願いします！

まとめ

今回は @ChocoLinkage さんの水滴を描くリンク機構をモデリングし、gnuplotでアニメーションを作ってみました

面白い、バズっているツイートを真似るのは勉強になりますし、モチベーションが比較的高い状態でプログラムを作成できるので良いですね。

今回作成したスクリプトとデモGIFは私のGitHubでも公開しています。英語で書いたREADMEもあるので、そちらも参考にしてみてください。

GitHub - hiroloquy/water-drop-linkage

Contribute to hiroloquy/water-drop-linkage development by cr...

github.com

リンク機構に興味のある方は以下の書籍がおすすめです。